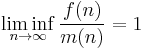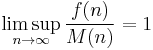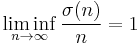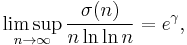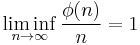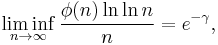Extremal orders of an arithmetic function

In mathematics, in number theory, the extremal orders of an arithmetic function are best possible bounds of the given arithmetic function. Specifically, if f(n) is an arithmetic function and m(n) is a non-decreasing function that is ultimately positive and

$\liminf_{n \to \infty} \frac{f(n)}{m(n)} = 1$

we say that m is a minimal order for f. Similarly if M(n) is a non-decreasing function that is ultimately positive and

$\limsup_{n \to \infty} \frac{f(n)}{M(n)} = 1$

we say that M is a maximal order for f.^[1]^:80 The subject was first studied systematically by Ramanujan starting in 1915.^[1]^:87

1 Examples
2 See also
3 Notes
4 Further reading

Examples

For the sum-of-divisors function σ(n) we have the trivial result

$\liminf_{n \to \infty} \frac{\sigma(n)}{n} = 1$

because always σ(n) ≥ n and for primes σ(p) = p + 1. We also have

$\limsup_{n \to \infty} \frac{\sigma(n)}{n \ln \ln n} = e^\gamma,$

proved by Gronwall in 1913.^[1]^:86^[2]^{:Theorem 323}^[3] Therefore n is a minimal order and e^−γ n ln ln n is a maximal order for σ(n).

For the Euler totient φ(n) we have the trivial result

$\liminf_{n \to \infty} \frac{\phi(n)}{n} = 1$

because always φ(n) ≤ n and for primes φ(p) = p − 1. We also have

$\liminf_{n \to \infty} \frac{\phi(n) \ln \ln n}{n} = e^{-\gamma},$

proved by Landau in 1903.^[1]^:84^[2]^{:Theorem 328}

For the number of divisors function d(n) we have the trivial lower bound 2 ≤ d(n), in which equality occurs when n is prime, so 2 is a minimal order. For ln d(n) we have a maximal order ln 2 ln n / ln ln n, proved by Wigert in 1907.^[1]^:82^[2]^{:Theorem 317}
For the number of distinct prime factors ω(n) we have a trivial lower bound 1 ≤ ω(n), in which equality occurs when n is prime. A maximal order for ω(n) is ln n / ln ln n.^[1]^:83
For the number of prime factors counted with multiplicity Ω(n) we have a trivial lower bound 1 ≤ Ω(n), in which equality occurs when n is prime. A maximal order for Ω(n) is ln n / ln 2.^[1]^:83

Notes

^ ^a ^b ^c ^d ^e ^f ^g Tenenbaum, Gérald (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge studies in advanced mathematics. 46. Cambridge University Press. ISBN 0-521-41261-7.
^ ^a ^b ^c Hardy, G. H.; Wright, E. M. (1979). An Introduction to the Theory of Numbers (5th ed.). Oxford: Clarendon Press. ISBN 0198531710.
^ Gronwall, T. H. (1913). "Some asymptotic expressions in the theory of numbers". Transactions of the American Mathematical Society 13 (4): 113–122.

Extremal orders of an arithmetic function

Contents

Examples

See also

Notes

Further reading